关于应用密码学最令人扼腕也最引人入胜的一件事就是我们在现实中实际使用的密码学是多么的少。这并不是指密码学在业界没有被广泛的应用————事实上它的应用很广泛。我想指出的是,迄今为止密码学研究人员开发了如此多实用的技术,但工业界平常使用的却少之又少。实际上,除了少数个别情况,我们现今使用的绝大部分密码学技术是在 21 世纪初 (注1) 就已经存在的技术。

大多数人并不在意这点,但作为一个工作在研究与应用交汇领域的密码学家,这让我感到不开心。我不能完全解决这个问题,我能做的,就是谈论一部分这些新的技术。在这个夏天里,这就是我想要做的:谈论。具体来说,在接下来的几个星期里,我将会写一系列讲述这些没有被看到广泛使用的前沿密码学技术的文章。
今天我要从一个非常简单的问题开始:在公钥加密之外还有什么(可用的加密技术)?具体地说,我将讨论几个过去 20 年里开发出的技术,它们可以让我们走出传统的公钥加密的概念的局限。
这是一篇专业的技术文章,但是不会有太困难的数学内容。对于涉及方案的实际定义,我会提供一些原论文的链接,以及一些背景知识的参考资料。在这里,我们的关注点是解释这些方案在做什么————以及它们在现实中可以怎样被应用。
基于身份的加密
在 20 世纪 80 年代中期,一位名叫 阿迪·萨莫尔 的密码学家提出了一个 全新的想法 。这个想法,简单来说,就是摒弃公钥。
为了理解 萨莫尔 的想法从何而来,我们最好先了解一些关于公钥加密的东西。在公钥加密的发明之前,所有的加密技术都牵涉到密钥。处理这样的密钥是相当累赘的工作。在你可以安全地通信之前,你需要和你的伙伴交换密钥。这一过程非常的困难,而且当通信规模增大时不能很好地运作。
公钥加密(由 Diffie-Hellman 和萨莫尔的 RSA 密码系统发展而来的)通过极大地简化密钥分配的过程给密码学带来了革命性的改变。比起分享密钥,用户现在只要将他们的公共密钥发送给其他使用者。有了公钥,公钥的接收者可以加密给你的信息(或者验证你的数字签名),但是又不能用该公钥来进行解密(或者产生数字签名)。这一部分要通过你自己保存的私有密钥来完成。
尽管公钥的使用改进了密码学应用的许多方面,它也带来了一系列新的挑战。从实践中的情况来看,拥有公钥往往只是成功的一半————人们通常还需要安全地分发这些公钥。
举一个例子,想象一下我想要给你发送一封 PGP 加密的电子邮件。在我可以这么做之前,我需要获得一份你的公钥的拷贝。我要怎么获得呢?显然我们可以亲自会面,然后当面交换这个密钥————但(由于面基的麻烦)没有人会愿意这样做。通过电子的方式获得你的公钥会更理想。在现实中,这意味着要么(1)我们必须通过电子邮件交换公钥, 要么(2)我必须通过某个第三方基础设施,比如一个 网站 或者 密钥服务器 ,来获得你的密钥。现在我们面临这样的问题:如果电子邮件或密钥服务器是不值得信赖的(或者简单的来说允许任何人以 你的名义 上传密钥 ),我就可能会意外下载到恶意用户的密钥。当我给“你”发送一条消息的时候,也许我实际上正在将消息加密发送给 Mallory.

Mallory
解决这个问题——关于交换公钥和验证它们的来源的问题——激励了大量的实践密码工程,包括整个 web PKI (网络公钥基础设施)。在大部分情况下,这些系统非常奏效。但是萨莫尔并不满意。如果,他这样问道,我们能做得更好吗?更具体地说,他这样思考:我们是否可以用一些更好的技术去替换那些麻烦的公钥?
萨莫尔的想法非常令人激动。他提出的是一个新的公钥加密形式,在这个方案中用户的“公钥”可以就是他们的身份。这个身份可以是一个名字(比如 “Matt Green”)或者某些诸如电子邮箱地址这样更准确的信息。事实上,“身份”是什么并不重要。重要的是这个公钥可以是一个任意的字符串————而不是一大串诸如“ 7cN5K4pspQy3ExZV43F6pQ6nEKiQVg6sBkYPg1FG56Not ”这样无意义的字符组合。
当然,使用任意字符串作为公钥会造成一个严重的问题。有意义的身份听起来很棒————但我们无法拥有它们。如果我的公钥是 “Matt Green” ,我要怎么得到的对应的私钥?如果我能获得那个私钥,又有谁来阻止其他的某些 Matt Green 获得同样的私钥,进而读取我的消息。进而考虑一下这个,谁来阻止任意的某个不是名为 Matt Green 的人来获得它。啊,我们现在陷入了 Zooko 三难困境 。
萨莫尔的想法因此要求稍微更多一点的手段。相比期望身份可以全世界范围使用,他提出了一个名为“ 密钥生成机构 ”的特殊服务器,负责产生私钥。在设立初期,这个机构会产生一个 最高公共密钥 (MPK),这个公钥将会向全世界公布。如果你想要加密一条消息给“Matt Green”(或者验证我的签名),你可以用我的身份和我们达成一致使用的权威机构的唯一 MPK 来加密。要解密这则消息(或者制作签名),我需要访问同一个密钥机构,然后请求一份我的密钥的拷贝。密钥机构将会基于一个秘密保存的 最高私有密钥 (MSK)来计算我的密钥。
加上上述所有的算法和参与者,整个系统看起来是这样的:
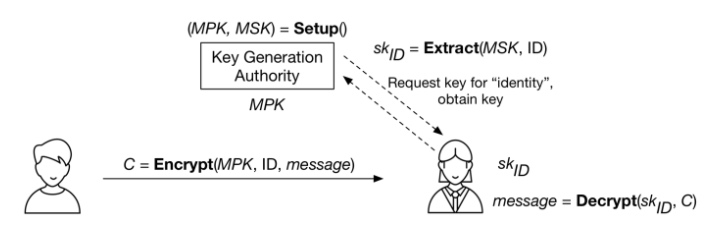
一个 基于身份加密 (IBE)系统的概览。 密钥生成机构 的 Setup 算法产生最高公共密钥(MPK)和最高私有密钥(MSK)。该机构可以使用 Extract 算法来根据指定的 ID 生成对应的私钥。加密器(左)仅使用身份和 MPK 来加密。消息的接受者请求对应她身份的私钥,然后用这个私钥解密。(图标由 Eugen Belyakoff 制作)
这个设计有一些重要的优点————并且胜过少数明显的缺点。在好的方面,它完全摆脱了任何和你发送消息的对象进行密钥交换的必要。一旦你选择了一个主密钥机构(然后下载了它的 MPK),你就可以加密给整个世界上任何一个人的消息。甚至更酷炫地,在你加密的时候,你的通讯对象甚至还不需要联系密钥机构。她可以在你给她发送消息之后再取得她的私钥。
当然,这个“特性”也同时是一个漏洞。因为密钥机构产生所有的私钥,它拥有相当大权力。一个不诚实的机构可以轻易生成你的私钥然后解密你的消息。用更得体的方式来说就是标准的 IBE 系统有效地“包含” 密钥托管机制。 (注2)
基于身份加密(IBE)中的“加密(E)”
所有这些想法和额外的思考都是萨莫尔在他 1984 年的论文中提出来的。其中有一个小问题:萨莫尔只能解决问题的一半。
具体地说,萨莫尔提出了一个 基于身份签名 (IBS)的方案—— 一个公共验证密钥是身份、而签名密钥由密钥机构生成的签名方案。他尽力尝试了,但仍然不能找到一个建立基于身份加密的解决方案。这成为了一个悬而未决的问题。 (注3)
到有人能解决萨莫尔的难题等了 16 年。令人惊讶的是,当解答出现的时候,它出现了不只一次,而是三次。
第一个,或许也是最负盛名的 IBE 的实现,是由 丹·博奈 和 马太·富兰克林Matthew Franklin在多年以后开发的。博奈和富兰克林的发现的时机十分有意义。 博奈富兰克林方案 根本上依赖于能支持有效的 “ 双线性映射 ” (或者“ 配对 ”) (注4) 的椭圆曲线。需要计算这些配对的该类 算法 在萨莫尔撰写他的那篇论文是还不被人知晓,因此没有被建设性地使用——即被作为比起 一种攻击 更有用的东西使用——直至 2000年。
(关于博奈富兰克林 IBE 方案的简短教学,请查看 这个页面)
第二个被称为 Sakai-Kasahara 的方案的情况也大抵类似,这个方案将在与第一个大约同一时间被另外一组学者独立发现。
第三个 IBE 的实现并不如前二者有效,但却更令人吃惊得多。这个方案 由 克利福德·柯克斯 ,一位英国国家通信总局的资深密码学家开发。它因为两个原因而引人注目。第一,柯克斯的 IBE 方案完全不需要用到双线性映射——都是建立在以往的 RSA 的基础上的,这意味着原则上这个算法这么多年来仅仅是没有被人们发现(而非在等待相应的理论基础)而已。第二,柯克斯本人近期因为一些甚至更令人惊奇的东西而闻名:在 RSA 算法被提出之前将近 5 年 发现 RSA 加密系统(LCTT 译注:即公钥加密算法)。用再一个在公钥加密领域的重要成就来结束这一成就,实在堪称令人印象深刻的创举。
自 2001 年起,许多另外的 IBE 构造涌现出来,用到了各种各样的密码学背景知识。尽管如此,博奈和富兰克林早期的实现仍然是这些算法之中最为简单和有效的。
即使你并不因为 IBE 自身而对它感兴趣,事实证明它的基本元素对密码学家来说在许许多多单纯地加密之外的领域都十分有用。事实上,如果我们把 IBE 看作是一种由单一的主公/私钥对来产生数以亿计的相关联的密钥对的方式,它将会显得意义非凡。这让 IBE 对于诸如 选择密文攻击 , 前向安全的公钥加密 和 短签名方案 这样各种各样的应用来说非常有用。
基于特征加密
当然,如果你给密码学家以一个类似 IBE 的工具,那么首先他们要做的将是找到一种让事情更复杂改进它的方法。
最大的改进之一要归功于 阿密特·萨海 和 布伦特·沃特世 。我们称之为 基于特征加密 ,或者 ABE。
这个想法最初并不是为了用特征来加密。相反,萨海和沃特世试图开发一种使用生物辨识特征来加密的基于身份的加密方案。为了理解这个问题,想象一下我决定使用某种生物辨识特征,比如你的 虹膜扫描影像,来作为你的“身份”来加密一则给你的密文。然后你将向权威机构请求一个对应你的虹膜的解密密钥————如果一切都匹配得上,你就可以解密信息了。
问题就在于这几乎不能奏效。
告诉我这不会给你带来噩梦
因为生物辨识特征的读取(比如虹膜扫描或者指纹模板)本来就是易出错的。这意味着每一次的读取通常都是十分接近的,但却总是会几个对不上的比特。在标准的 IBE 系统中这是灾难性的:如果加密使用的身份和你的密钥身份有哪怕是一个比特的不同,解密都会失效。你就不走运了。
萨海和沃特世决定通过开发一种包含“阈值门”的 IBE 形式来解决这个问题。在这个背景下,一个身份的每一个字节都被表示为一个不同的“特征”。把每一个这种特征看作是你用于加密的一个元件——譬如“你的虹膜扫描的 5 号字节是 1”和“你的虹膜扫描的 23 号字节是 0”。加密的一方罗列出所有这些字节,然后将它们中的每一个都用于加密中。权威机构生成的解密密钥也嵌入了一连串相似的字节值。根据这个方案的定义,当且仅当(你的身份密钥与密文解密密钥之间)配对的特征数量超过某个预先定义的阈值时,才能顺利解密:比如为了能解密,2048 个字节中的(至少) 2024 个要是对应相同的。
这个想法的优美之处不在于模糊 IBE,而在于一旦你有了一个阈值门和一个“特征”的概念,你就能做更有趣的事情。主要的观察结论 是阈值门可以拥有实现布尔逻辑的 AND 门和 OR 门(LCTT 译注:译者认为此处应为用 AND 门和 OR 门实现, 原文: a threshold gate can be used to implement the boolean AND and OR gates),就像这样:
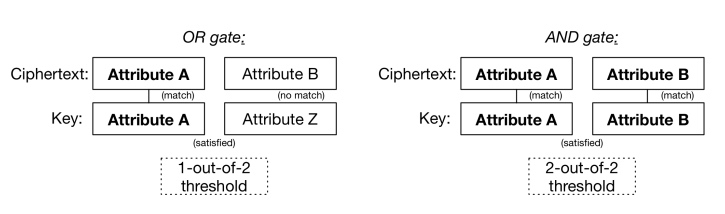
甚至你还可以将这些逻辑闸门堆叠起来,一些在另一些之上,来表示一些相当复杂的布尔表达式——这些表达式本身就用于判定在什么情况下你的密文可以被解密。举个例子,考虑一组更为现实的特征,你可以这样加密一份医学记录,使医院的儿科医生或者保险理算员都可以阅读它。你所需要做的只不过是保证人们可以得到正确描述他们的特征的密钥(就是一些任意的字符串,如同身份那样)。
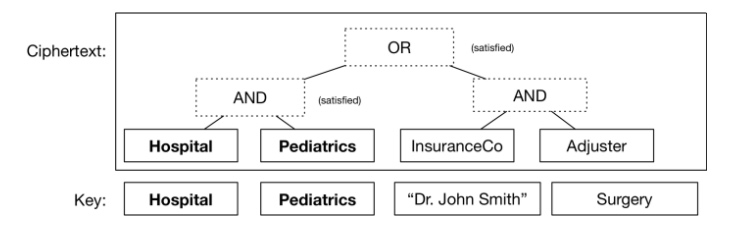
一个简单的“密文规定”。在这个规定中当且仅当一个密钥与一组特定的特征匹配时,密文才能被解密。在这个案例中,密钥满足该公式的条件,因此密文将被解密。其余用不到的特征在这里忽略掉。
其他的条件判断也能实现。通过一长串特征,比如文件创建时间、文件名,甚至指示文件创建位置的 GPS 坐标, 来加密密文也是有可能的。于是你可以让权威机构分发一部分对应你的数据集的非常精确的密钥————比如说,“该密钥用于解密所有在 11 月 3 号和 12 月 12 号之间在芝加哥被加密的包含‘小儿科’或者‘肿瘤科’标记的放射科文件”。
函数式加密
一旦拥有一个相关的基础工具,像 IBE 和 ABE,研究人员的本能是去扩充和一般化它。为什么要止步于简单的布尔表达式?我们能不能制作嵌入了任意的计算机程序的 密钥 (或者 密文 )?答案被证明是肯定的——尽管不是非常高效。一组 近几年的 研究 显示可以根据各种各样的 基于格 的密码假设,构建在 任意多项式大小线路 运作的 ABE。所以这一方向毫无疑问非常有发展潜力。
这一潜力启发了研究人员将所有以上的想法一般化成为单独一类被称作 “函数式加密” 的加密方式。函数式加密更多是一种抽象的概念而没有具体所指——它不过是一种将所有这些系统看作是一个特定的类的实例的方式。它基本的想法是,用一种依赖于(1)明文,和(2)嵌入在密钥中的数据 的任意函数 F 的算法来代表解密过程。
(LCTT 译注:上面函数 F 的 (1) 原文是“the plaintext inside of a ciphertext”,但译者认为应该是密文,其下的公式同。)
这个函数大概是这样的:
输出 = F(密钥数据,密文数据)
在这一模型中,IBE 可以表达为有一个加密算法 加密(身份,明文)并定义了一个这样的函数 F:如果“密钥输入 == 身份”,则输出对应明文,否则输出空字符串的系统。相似地,ABE 可以表达为一个稍微更复杂的函数。依照这一范式,我们可以展望在将来,各类有趣的功能都可以由计算不同的函数得到,并在未来的方案中被实现。
但这些都必须要等到以后了。今天我们谈的已经足够多了。
所以这一切的重点是什么?
对于我来说,重点不过是证明密码学可以做到一些十分优美惊人的事。当谈及工业与“应用”密码学时,我们鲜有见到这些出现在日常应用中,但我们都可以等待着它们被广泛使用的一天的到来。
也许完美的应用就在某个地方,也许有一天我们会发现它。
注:
- 注 1:最初在这片博文里我写的是 “20 世纪 90 年代中期”。在文章的评论里,Tom Ristenpart 提出了异议,并且非常好地论证了很多重要的发展都是在这个时间之后发生的。所以我把时间再推进了大约 5 年,而我也在考虑怎样将这表达得更好一些。
- 注 2:我们知道有一种叫作 “无证书加密” 的加密的中间形式。这个想法由 Al-Riyami 和 Paterson 提出,并且使用到标准公钥加密和 IBE 的结合。基本的思路是用一个(消息接受者生成的)传统密钥和一个 IBE 身份共同加密每则消息。然后接受者必须从 IBE 权威机构处获得一份私钥的拷贝来解密。这种方案的优点是两方面的:(1)IBE 密钥机构不能独自解密消息,因为它没有对应的(接受者)私钥,这就解决了“托管”问题(即权威机构完全具备解密消息的能力);(2)发送者不必验证公钥的确属于接收者(LCTT 译注:原文为 sender,但译者认为应该是笔误,应为 recipient),因为 IBE 方面会防止伪装者解密这则消息。但不幸的是,这个系统更像是传统的公钥加密系统,而缺少 IBE 简洁的实用特性。
- 注 3:开发 IBE 的一部分挑战在于构建一个面临不同密钥持有者的“勾结”安全的系统。譬如说,想象一个非常简单的只有 2 比特的身份鉴定系统。这个系统只提供四个可能的身份:“00”,“01”,“10”,“11”。如果我分配给你对应 “01” 身份的密钥,分配给 Bob 对应 “10” 的密钥,我需要保证你们不能合谋生成对应 “00” 和 “11” 身份的密钥。一些早期提出的解决方法尝试通过用不同方式将标准公共加密密钥拼接到一起来解决这个问题(比如,为身份的每一个字节保留一个独立的公钥,然后将对应的多个私钥合并成一个分发)。但是,当仅仅只有少量用户合谋(或者他们的密钥被盗)时,这些系统就往往会出现灾难性的失败。因而基本上这个问题的解决就是真正的 IBE 与它的仿造近亲之间的区别。
- 注 4: 博奈和富兰克林方案的完整描述可以在 这里 看到,或者在他们的 原版论文 中。这里、这里 和 这里 有一部分代码。除了指出这个方案十分高效之外,我不希望在这上面花太多的篇幅。它由 Voltage Security(现属于惠普) 实现并占有专利。
via: https://blog.cryptographyengineering.com/2017/07/02/beyond-public-key-encryption/
作者:Matthew Green 译者:Janzen_Liu 校对:wxy


发表回复